Functions and Mapping SS3 Mathematics Lesson Note

Definition: This is the rule which assigns an element x in set A to another unique element y in set B.

Set A is called the Domain while set B is the Co-domain. 

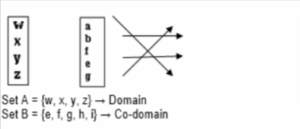
Image: This is the unique element in set B produced by an element in set A.

Range: This is the collection of all the images of the elements of the domain.

Using the diagram above:

f(w)= g, f(x)= b, f(y)=f, f(z)=a

a, b, f and g are the images of elements a,b,c and d respectively.

Range = {a, b, f, g,}

The rule which associates each element in set A to a unique element in set B is denoted by any

of the following notations: f: A → B or f: A→ B 

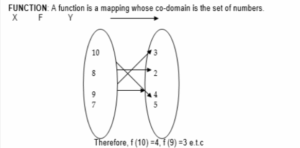
Example 1: Given f(x) = 3x² + 2, find the values of (a) f (4) (b) f (-3) (c) f (-1/2)

SOLUTION:

F(x) = 3x²+ 2

(a)

F(4), i.e x=4

F(4) = 3(4²) + 2 = 3(16) + 2

= 48 + 2

= 50

(b)

F(-3) = 3(-3)²+2

= 3(9) +2 = 27 +2

= 29

(c) F(-1/2) = 3(-1/2)²+ 2

= 3(1/4) + 2 = 3+ 2

4

=11/4.

Example 2: Determine the domain D of the mapping, g:x→ 2x² – 1, if R= {1,7,17} is the

range and g is defined on D.

SOLUTION:

g(x) = 2x²- 1,

R = {1,7,17}

To find the domain, when g(x) = 1,

$$

\begin{aligned}

1 &= 2x²-1\\

1+1 &= 2x²\\

x² &= 2/2

\end{aligned}

$$

x=1

When g(x) = 7,

$$

\begin{aligned}

7 &= 2x²-1\\

7+1 &= 2x²\\

8 &=2x²\\

x²&= 4,

\end{aligned}

$$

x= 2

When g(x) = 17,

$$

\begin{aligned}

17 &=x²-1\\

17+1 &= 2x²\\

18 &=x²

\end{aligned}

$$

x² = 9,

x= 3

Domain D ={1, 2,3}

EVALUATION

1. Given f(x) = x²+ 4x +3 find the values of.

(a) f(2) (b) f(1/2) (c) f(-3)

1. Given that f(x) = ax + b and that f(2) = 7,f(3) = 12. Find a and b.

TYPES OF MAPPING

One-One mapping: A mapping is one-one if different elements in the domain have different

images in the co-domain. If x₁= X2 then f(X1) = f(x2)

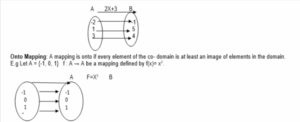
The mapping is one-on-one.

NB: In an onto mapping, the range is the same as the co-domain.

**Identity Mapping:** This is a mapping that takes an element onto itself. If f: x→ x is a mapping

such that f(x) = x for all x € X.