Games Theory SS3 Further Mathematics Lesson Note

Game Theory is a set of concepts aimed at decision-making in situations of competition or conflicts (as well as of cooperation and interdependence) under specified rules. It is a decision theory which is applicable to competitive situations.

COMPETITIVE GAME: This is the competitive situations which occur between two or more persons.

PROPERTIES OF A COMPETITIVE GAME

• The number of participants is stated or finite.
• Each action of operations of individuals is certain
• The choices of players are made simultaneously, for the participants’ choices to be personal to the others until he makes his decision.
• The players of the games must know all the courses of action available but must not know which of these courses will be chosen.       TYPES OF GAMES

• One-person games
• Two-person games
• Two-person zero-sum games
• N-person games.

ONE-PERSON GAMES

This is a game that consists of one player. There is no competition or conflict in this because the interest of the only player is at stake. i.e. solitaire game.

TWO-PERSON GAMES

This involves two players who have conflicting interests. Each player has several possible choices open to them at each play of the game. E.g. checkers, chess etc.

N-PERSON GAMES

This involves unspecified numbers of players. E.G. POKER (board and card games), monopoly games etc.

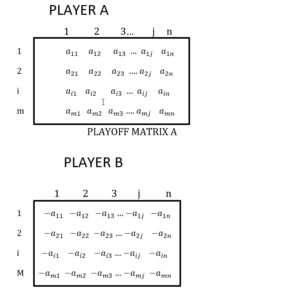
PAYOFF (OUTCOME) MATRIX

This is an expression of the first law of decision science. Each row represents one action that the decision maker might or might not freely choose to perform while each column represents a possible state of nature.

Given two players A and B, if the outcome is positive, then it represents a gain to player A and a loss to player B. But if  is negative, then it represents a loss to A but a gain to B