Calculating Distances Using Longitude, Latitude & Great Circles SS3 Mathematics Lesson Note

SPECIFIC OBJECTIVES: At the end of the lesson, the student should be able to: 

1. Give the formula for finding distance along the parallel of longitude or great circle.
2. Solve problems involving longitude or great circles.
3. give the formula for finding distance along the parallel of latitude 
4. Solve problems involving latitude

INSTRUCTIONAL RESOURCES Real globe and an Orange.B.

PRESENTATION:

The teacher presents the lesson with the steps below:

STEP I    Identification of prior ideas.

Mode:  Entire students

Teacher’s Activities: Displays instructional resources and instructs the students to identify the lines of longitude afterwards leads students to give the formula for determining distance along a parallel of longitude or great circle.

Students’ Activities: Students identify the lines on longitude and give the formula for determining the parallel of longitude or great circle.

Lines of Longitudes

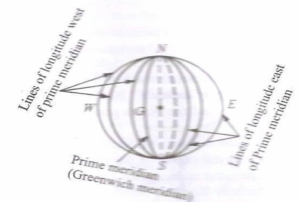
The formula for calculating distance along a parallel of longitude or great circle.

Distance. = ө/360 x 2πr cos latitude°

STEP II:              Exploration

Mode: Individual

Teacher’s Activities: Leads students to solve problems involving longitude or great circle

Students’ Activities: Students solve problems involving longitude or great circle

Towns A and B lie on the equator. A has longitude 63° E. While B has longitude 123°E. What is the difference between the two towns along the equator?

1. How far is Santa from the North Pole? (Take the radius of the Earth is 6400).

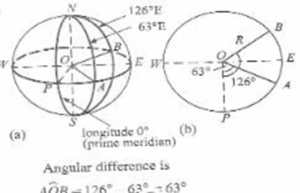
Arc AB = 63/360. x2πR. = 2 x 22 x 160 km = 7040 km

(b) distance from the North Pole = arc AN. The angular difference is 90°

Therefore, Arc AN = 90/360 x 2πR. = 90/360 x 2 x 22/7 x 6400 km = 10057 km.

STEP III: Discussion

Mode:  Individual

Teacher’s Activities: Displays instructional resources and instructs the students to identify the lines of latitude afterwards leads students to give the formula for determining distance along parallel latitude.

Students’ Activities: Students identify the lines on latitude and give the formula for determining the parallel of latitude

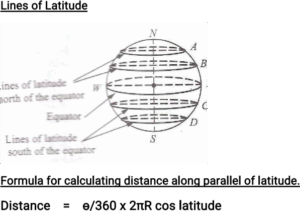
Where: ө is the angular difference, and cos latitude is the angle formed at the parallel of

22/

latitude and use R = 6400 km where not given. π =      7

STEP IV: Application

Mode: Individual

Teacher’s: Leads students to solve problems involving latitude.

Students’ Activities: Students solve problems involving latitude.

1. Find the longitude difference between A( 06°N, 40°W) and B(60°N, 70°E)
2. Find the distance measured along the parallel of latitude between A And B

( Take the radius of the Earth =l 6400 KM and π =22/7

1. Calculate the difference in longitude between the following places 

• P( 48° N, 25°E) and Q( 48°N, 58°E). 
• X(65°S, 40°E) and Y(65°S, 32°W) 

1. Calculate the difference in latitude between the following places.

• P( 49°N, 50°E) and Q(30°S, 50°E). 
•  X( 60°N, 32°W) and Y(20°N, 32°W)

CONCLUSION: The teacher goes around to assess the student’s work and gives corrections on the board for students to copy.

ASSIGNMENT:

Calculate the distances between the places given in evaluation questions (a) and (b) above

REFERENCES:

1. Bakare L. Niyi, 2014, Mathematics Clinic
2. Essential Mathematics for SS 3 students.