Surface Area and Volume of Sphere and Hemispherical Sphere Volume SS3 Mathematics Lesson Note
Download Lesson NoteTopic: Surface Area and Volume of Sphere and Hemispherical Sphere Volume
MENSURATION Is defined as a branch of Mathematics that deals with measurement, especially the derivation and use of algebraic formulae to measure the areas, volumes and different parameters of geometry. Examples are cylinder, cone, cuboid, rectangular prism, rectangular-based pyramid, the total surface area of cylinder, cone and their volume.
FORMULAE
| SHAPES | AREA | SURFACE AREA (C.S.A) | TOTAL SURFACE AREA (T.S.A) | VOLUME |
| CONE | rl | rl | l + r) | |
| CYLINDER | 2 rh | 2 rh+2 | ||
| CUBOID | 2(lb+lh+bh) | l.b.h | ||
| TRIANGULAR PRISM | The sum of areas of all surfaces | Area of cross section x height | ||
| RECTANGULAR PYRAMID | The sum of all four triangular faces + base area | x base area x height | ||
| CUBE | 6 | |||
| SPHERE | 4πR2 | πR3 | ||
| HEMISPHERE | 2πR2 | 3πR2 | 4πR3 |
SPHERE

A HEMISPHERE
Volume of a Sphere
A sphere is a solid in which all the points on the round surface are equidistant from a fixed point, known as the centre of the sphere. The distance from the centre to the surface is the radius.
The volume of the sphere = where r is the radius.
How to find the volume of a sphere? What is the volume of air in the ball?
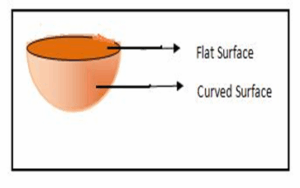
The volume of a hemisphere
A hemisphere is half a sphere, with one flat circular face and one bowl-shaped face.
The volume of the hemisphere where r is the radius
Spheres
What is a sphere?
A sphere is solid with all its points the same distance from the centre. The distance is known as the radius of the sphere. The maximum straight distance through the centre of a sphere is known as the diameter of the sphere. The diameter is twice the radius.
How to find the volume of a sphere?
The volume of a sphere is equal to four-thirds of the product of pi and the cube of the radius.
The volume and surface area of a sphere are given by the formulas:
where r is the radius of the sphere.
Example:
Calculate the volume of the sphere with radius 4 cm.
Solution:
Volume of sphere
We can also change the subject of the formula to obtain the radius given the volume.
Example 1: The volume of a spherical ball is 5,000 cm3. What is the radius of the ball?
Example2: Find the volume of a sphere with a diameter of 14 cm.





















