Graph Of Linear Inequality In Two Variables SS2 Mathematics Lesson Note

The term inequality applies to any statement involving one of the symbols.  Similar to ordinary equations, inequality equations too have solutions.

RULES FOR FINDING THE SOLUTIONS TO INEQUALITY EQUATIONS

1. Add or subtract the same expression or number to both sides of the inequality and preserve the inequality sign.
2. Multiply or divide both sides of the inequality by the same positive number and preserve the inequality sign.
3. Multiply or divide both sides of the inequality by the same negative number and reverse the inequality sign.

The expression 3x – 1 > x + 1 is a linear inequality in one variable x.  Thus, a linear inequality in x is an inequality in which the highest power of x is one (unity).

Solve the following linear inequality and represent them on a number line.

A number line is used to illustrate linear inequalities in one variable.  A point x = a divides the number line into 2 parts, x < a and x > a

But when x = a is included, the number line becomes 

A line segment from a to be is denoted by a  and it is shown below

i. 4x + 8 < 3x + 16

Subtract 8 from both sides

4x + 8 – 8 < 3x – 8 + 16

4x < 3x + 8

Subtract 3x from both sides

4x – 3x < 3x + 8 – 3x

X < + 8

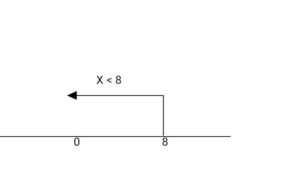
ii. 3 (x – 6)  9 (x – 1)

open the brackets

3x – 18  9x – 9

Collect like terms

3x – 9x  -9 + 18

-6x  + 9

Divide through by -6 and change the sign.

-6 > -9

 6      6

X  > -3 

         2

(x > 2³/⁷)