Trigonometric Ratios – SS2 Mathematics Lesson Note (Second Term)

Determination of lengths of chords using trigonometric ratios

Trigonometric ratios can be used to find the length of chords of a given circle.  However, in some cases where angles are not given.

Pythagoras theorem is used to find the lengths of chords in such cases.

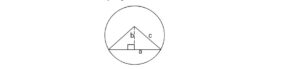
Pythagoras theorem is stated as follows:

It states that c2 = a2 + b2

Pythagoras’ theorem states that in a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the square of the lengths of the other two sides.

Examples

1. A chord is drawn 3cm away from the centre of a circle of radius 5cm. Calculate the length of the chord.
2. In a figure, O is the centre of the circle, HKL.  HK = 16cm, HL = 10cm and the perpendicular from O to the HK is 4cm.  What is the length of the perpendicular from O to HL?

Solution:

1. Sketch a right-angled triangle and label it correctly. 

|AB|^2  + 3^2  = 5^2  ( Pythagoras theorem)

|AB|^2 =  5^2 – 3^2

 |AB|^ 2 = 2^5 – 9

|AB| ^ 2  = 16

 AB    = √16 = 4cm  

Since B is the midpoint of chord AC then: 

Length of chord AC = 2 x AB  

 = 2x 4cm =8cm

2. Let the distance from O to HL= xcm

In right-angled triangle OMH:

 |OH|^2  = |HM|^2   + |MO| ^2

|OH|^2=  8^2 + 4^2

 =  64  + 16

= 80

:.         |OH|  = √80  

:.           OH   = √80cm

 but   OH   = radius of the circle 

i.e r=   OH     =   OL  = √80cm

In a right-angled triangle  ONL

OL  2  =    ON 2   +   NL 2

i.e( √80)2 = x2 + 52

80- 25 = x2

55 = x2

Take the square root of both sides 

√55   = √x2

√55 = x = 7. 416cm 

:. The length of the perpendicular from O to HL is 7.416cm