Straight Lines Graphs SS2 Mathematics Lesson Note

In coordinate geometry, we make use of points in a plane.  A point consists of the x-coordinate called abscissa and the y-coordinate known as ordinate.  In locating a point on the x – y plane. x – coordinate is first written and then the y-coordinate.  For example, in a given point (a, b), the value of x is a and that of y is b.  Similarly, in a point (3, 5), the value of x is 3 and that of y is 5.  

A linear graph gives a straight line graph from any given straight line equation which is in the general form y = mx + c or ax + by + c = 0

Example: Draw the graph of equation 4x + 2y = 5

i. Point of intersection of two linear equations

Two lines y = ax +b and y2 = cx + d 

Intercept when ax + b = cx + d

That is you solve the two equations simultaneously 

ii. Intersection of a line with the x or y axis

The point of intersection of a line with the x –axis can be obtained by putting y = o to find the corresponding value of x = a, say the required point of intersection gives (a, o).  Similarly, for the point of intersection of a line with the y-axis, put x = o to find the corresponding value of y.  If the corresponding value of y is b, the required point of intersection is (o, b)

Example: Find the point of intersection of the line 2x + 3y + 2 = 0 with the 

1. x – axis (ii) y – axis 

Example 3: Find the point of intersection of the lines y = 3x + 2 and y = 2x + 5

Solution

y = 3x + 2 (1)

y = 2x + 5 (2)

At the point of intersection

3x + 2 = 2x + 5

3x – 2x = 5 -2

X = 3

Substitute 3 for x in equation (1), we obtain y = 3(3) + 2 = 11.

Hence, the point of intersection is (3, 11)

GRADIENT OF A STRAIGHT LINE 

The Gradient of a straight line is defined as the ratio

Change in y in moving from one 

Change in x point to another on the line.  The Gradient of a straight line is always constant.

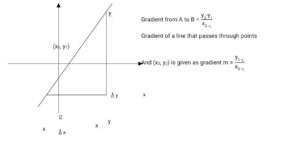
Meaning that the gradient of the line is the ratio of increase in y to increase in x.

TANGENT OF ANGLE OF SLOPE

In the above diagram, tan  = .

Since  = y2 – y1   

tan  =  = m

And  = x2 – x1

tan  = m.  It then follows that the gradient of a line can be defined as tangent of angle of slope.

Example:

Calculate the gradient and the angle of slope of the line passing through (1, 3) and (-4, 2)

EQUATION OF A STRAIGHT LINE AND TANGENT TO A CURVE 

EQUATION OF A STRAIGHT LINE

Equation of a line with gradients in m and y intercept c.  Equation of a line with gradient m and y intercept c is given as y = mx + c.

i. Equation of a line passing through the point (x1, y1) with gradient.

The general equation of a line with known gradient m and which passes through the point (x1,y1) is given as m = y  – y1

       x     x1

Example 2

The equation of the line with gradient 2 and which passé through the point (-3, 2).

The solution (equation) of a line with known gradient and passing through the point (x1, y1) is given by  y  –  y1

                                                x      x1

Here, m = 2, (x1, y1) = (-3, 2)

The required equation of the line is 

   y – 2   = 2

  x – (-3)

y – 2 = 2

x + 3 

y – 2 = 2(x + 3)

y = 2x + 6 + 2

y = 2x + 8

y = 2x + 8

ii. Equation of a line passing through two given points

The equation of a line passing through two given points (x1, y1) and (x2, y2)

Is   = y – y1 = y2 – y1

         x – x1    x2 – x1

iii. Double Intercept form of the equation of a line. The equation of a line which has an intercept “a” on the x – axis and intercept “b” on the y-axis is given by  x + y = 1

                               a    b

Double Intercept Form Of The Equation Of A Line

The Equation of a line which has an intercept ‘a’ on the axis and intercept ‘b’ on the y-axis is given by x + y = 1

                                              a    b 

iv. Equation of a line passing through a point and making an angle  with the horizontal axis.

The equation of a line passing through the point (x1, y1) and making an angle  with the horizontal axis is    = tan  or y – y1 = (x – x1) tan.

Drawing Tangents To A Curve

The gradient at any particular point on a curve is defined as being the gradient of the tangent to the curve at that point the gradient of the curve at point A is the gradient of the tangent BA, that is, tan. The tangent is drawn by placing a ruler against the curve at A and drawing a line considering that the angels between the line and the curve are equal.  

(Note: Gradient to the horizontal line of a curve is zero because the tangent is horizontal known as a turning points (maximum/minimum)

ASSIGNMENT 

The gradients of a straight line is given as gradient = change in y / change in x.

The gradient of a curve at a point is given by the gradient of the tangent at that point.

The gradient at a turning point of any quadratic equation equals zero.

Exercise 14.5 no 1; the figure below (the text recommended) represents the graph of the function y = x2 + 4x – 5, 

1. a) Use the given tangents to find the gradient of the curve at (i) A (ii) B.

(b) Use the Graph to find the roots of the function.

1. c) State the equation of the line of symmetry of the curve.