Inequalities SS2 Mathematics Lesson Note

The term inequality applies to any statement involving one of the symbols.  Similar to ordinary equations, inequality equations too have solutions 

RULES FOR FINDING THE SOLUTIONS TO INEQUALITY EQUATIONS

1. Add or subtract at the same expression or number to both sides of the inequality and preserve the inequality sign.
2. Multiply or divide both sides of the inequality by the same positive number and preserve the inequality sign.
3. Multiply or divide both sides of the inequality by the same negative number and reverse the inequality sign.

The expression 3x – 1 > x + 1 is a linear inequality in one variable x.  Thus, a linear inequality in x is an inequality in which the highest power of x is one (unity).

Solve the following linear inequality and represent them on a number line.

A number line is used to illustrate linear inequalities in one variable.  A point x = a divides the number line into 2 parts, x < a and x > a

But when x = a is included, the number line becomes 

A line segment from a to be is denoted by a  and it is shown below

i. 4x + 8 < 3x + 16

Subtract 8 from both sides

4x + 8 – 8 < 3x – 8 + 16

4x < 3x + 8

Subtract 3x from both sides

4x – 3x < 3x + 8 – 3x

X < + 8

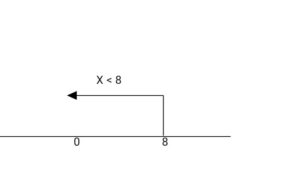
ii. 3 (x – 6)  9 (x – 1)

open the brackets

3x – 18  9x – 9

Collect like terms

3x – 9x  -9 + 18

-6x  + 9

Divide through by -6 and change the sign.

-6 > -9

 6      6

X  > -3 

         2

(x > 2³/⁷)

SOLUTIONS OF INEQUALITIES OF TWO VARIABLES AND THE RANGE OF VALUES OF COMBINED INEQUALITIES

A linear inequality in two variables x and y is of the form: ax + by   c:  ax + by < c:    ax + by > c    ax + by  c where a, b and c are constants.  A solution to an inequality is any pair of number x and y that satisfies the inequality.

Example:

Determine the solution set of 5x + 2y  17.

Solution

One solution to 5x + 2y < 17 is x =2 and y = 3 because 5(2) + 2(3) = 16, which is indeed less than 17.  But the pair x = 2 and y = 3 is not the only solution.  As a matter of fact, there are infinitely many solutions.  If the pairs of numbers x and y is a solution, then think of this pair as a point in the plane, so the set of all solutions can be thought of as a REGION in the x –y plane.

Hence, to illustrate how to determine this region, first express y in terms of x in the inequality.

3x + 2y  17

2y  -5x + 17

Y < -5x + 17

         2      2 

When x = 0, y = 8.5; when y = 0, x = 3  (show in a graph)