Circle Theorem SS2 Mathematics Lesson Note

ANGLES AT THE CENTRE OF A CIRCLE

Theorem 1

The angle which an arc of a circle subtends at the centre of a circle is twice that which it subtends at any point on the circumference of the circle.

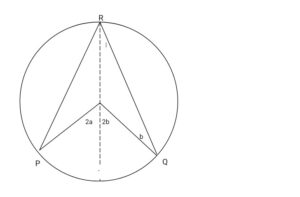
Given: A circle PQR, centre O.

To prove that P Ô Q = 2 P R Q

Construction: Join RO, and extend to any point T.

Proof: Po =Ro= Qo (radii)

a = a1 (base <s of Isos.  POR)

 P Ô Q = a + a1 = 2a (end <s of   POR)

But P Ô T + Q Ô T

Reflex of P Ô Q = 2a + 2b = 2(a +b) = 2 PRQ 

 angle at centre = 2 x (at circum. Of a circle).

Corollary 

The angle is a semi circle is a right angle 

Given: A semi circle3 P Q R, Centre O.

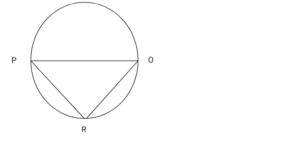
To prove that: PRO = 900

Construction: None

Proof: PQ is a diameter (given)

 P Ô Q = 1800

(< at centre = twice <s in circumference)

 2PRO = 180o

Hence PRO =  = 900 as required.

Theorem 2

Angles in the same segment of a circle and equal

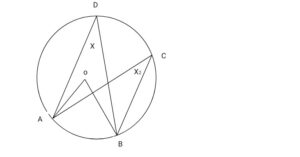
Given: points on a circle ABCD, AB is an arc of the circle.

To prove that: AD B = AC B

Construction: Join D and C to A and B, as shown above 

Proof: A Ô B = 2(x1 + x2)

X1 =  (A Ô B)

A D B = A C B as required.

CYCLIC QUADRILATERALS

A cyclic quadrilateral is a four-sided figure whose vertices lie in side and touch the circumference of the circle.  The opposite angles of C Cyclic quadrilateral lie in the opposite segment of the circle

Theorem 3

Opposite angles of a cyclic quadrilateral are supplementary.

Given: A cyclic quadrilateral PQRS

To prove that: P Q R + P S R = 180o

Construction: Join PO and RO of the circle.

Proof; P Ô R = 2y (< at Centre = twice  on the circumf.)

 2x + 2y = 360o (<s at a point)

2(x +y) = 360o

X + y = 180o

P ÔR + PSR = 180o 

ASSIGNMENT

Prove that if a straight line touches a circle a circle at a point, and from the point of contact a chord is drawn then the acute angles which this chord makes with the tangents are equal to the angle in the alternate segment