Surface Area And Volume Of Solid Shapes SS1 Mathematics Lesson Note
Download Lesson NoteTopic: Surface Area And Volume Of Solid Shapes
MENSURATION OF SOLID SHAPES
Properties Of Solid Shapes
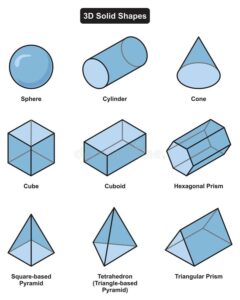
a) A Cube
A cube has the following properties.
i. It has 12 straight edges
ii. It has 8 vertices
iii. It also has 6 square faces
iv. Its net consists of 6 square faces joined together
b) A Cuboid
A cuboid has the following properties.
i.It has 12 straight edges
ii It has 8 vertices
iii. It also has 6 rectangular faces
iv. Its net consist of 6 rectangular faces
c) A Triangular Prism
A triangular prism has the following properties:
i. It has 6 vertices
ii. It has 9 straight edges
iii. It also has 3 rectangular faces and two triangular faces which are the end faces
iv. Its net consist of 3 rectangles and 2 triangles joined together
d) A Cylinder
Properties:
i. A cylinder has 2 circular faces
ii.It has 1 curved surface
iii. It has 2 curved edges
iv. Its net consists of two circular faces and 1 rectangular face i.e. its net consist of 2 circles and 1 rectangle.
e) A Cone
A cone has the following properties:
i. It has one vertex
ii. It has 2 curved edges
iii. It has 1 curved surface
iv. It also has 1 circular face
v. Its net consists of a sector of a circle and a circle
f) Rectangular based pyramids
A rectangular-based pyramid has the following properties:
i. It has 8 straight edges
ii. It has 5 vertices
iii. It has 4 triangular faces
iv. It has 1 rectangular face
v. Its net consists of 4 triangles and 1 rectangle
SURFACE AREA AND VOLUME OF COMMON SOLID SHAPES
A prism is a solid which has a uniform cross-section. Cubes, cuboids, and cylinders are examples of prisms. In general,
Volume of prism = area of uniform cross-section X perpendicular height = area of base x height
NOTE: The general formula for solid shapes is as follows:
- a) Cube
Volume = l3
Surface area = 6l^2
- b) Cuboid
Volume =lbh
Surface area = 2 (lb + lh + bh)
- c) Cylinder
Volume = πr^2 h
Curved surface area = 2πrh
Total surface area = 2πrh + 2π r^2
= 2πr ( h + r)
SURFACE AREA OF A CONE
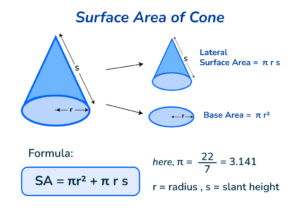
A sector of a circle can be bent to form the curved surface of an open cone. In the figure below, the sector OA x B is of radius l and arc A X B subtends angle θ at O. This sector is bent to form a cone of base radius r and slant height
The following points should be noted
The area of the sector is equal to the area of the curved surface of the cone.
The length of arc A x B is the same as the circumference of the circular base of the cone.
Curved surface area of cone =θ x πl2 ÷ 360°
Also,
θ x 2πl = 2 πr
360
Divide both sides by 2π
θ x 2πl = 2 πr
360 2π 2π
θ x l =r
360
divide both sides by l
θ = r
360 l
substitute r/l for θ in equation i) above:
360
Curve surface area of cone =r x πl2
l
= Πrl
Hence,
Total surface area = curved surface area of a cone + area of circular base
= πr l +π r2
= πr ( l + r)
Example:
- A paper cone has a diameter of 8cm and a height of 3cm
a). Sketch the cone and hence use Pythagoras theorem to calculate its slant height.
b). Calculate the curved surface area of the cone in terms of π
- c) If the cone is cut and opened out into the sector of a circle. What is the angle of
the sector?
- d) Assuming that the paper cone is closed at its base, what will be the total surface area of the closed paper cone?
Solution:
From the given information about the paper cone,
Diameter = 8cm
:. Radius = diameter ÷ 2
= 8cm = 4cm
2
using Pythagoras’ theorem in the right-angled triangle OBC
l2 = /OB/2 + /BC/ 2
l2 = 32 + 42
l2 = 9 + 16
l2 = 25
Take the square root of both sides
√ l2 =√ 25
l = 5cm
: The slant height of the paper cone is 5cm
- b) Curve surface area of the cone = πrl
= π x 4 x 5 cm
= 20 πcm2
- c) If the paper cone is cut and opened out into the sector of a circle as shown in the figure above, then
area of sector of circle = curved surface area of the cone
i.e θx π x (5) 2 = 20 x π
360
5
θx π x 25 = 20 x π
360
12
5 θ = 72 x 20
Divide both sides by 5
5 θ =72 x 20
5
5 θ = 72 x 4
θ = 288°
Volume of Pyramids and Volume of Cone
In general,
Volume = 1/3 x base area x height
SQUARE-BASED PYRAMID, RECTANGULAR-BASED PYRAMID AND CONE
:. The volume of square based pyramid = 1/3 x b2 x h
volume of the based pyramid = 1/3 x l x b x h
volume of the cone = 1/3 x Πr2 x h
Examples
- A pyramid 8cm high stands on a rectangular base 6cm by 4cm. Calculate the volume of the pyramid.
- A right pyramid on a base 4cm square has a slanted edge of 6cm. Calculate the volume of the pyramid.
- Calculate the volume of a cone 14cm in base diameter and 24cm high.
Solutions:
- Volume of a rectangular based pyramid = 1/3 x l x b x h
= 1/3 x 6 x 4 x 8 cm3
= 8 x8 cm3
= 64cm3
2) Considering the square base ABCD
/DB/ 2= /DC/ 2 + /CB/2
Pythagoras rule:
/DB/2 = 42 + 42
/B/2 = 16 + 16.
:. √/DB/ = √ 32
/DB/ = 4 √2 cm
but
/ EB/ = ½ /DB/
Since t is the midpoint of / DB/
Then /EB/ = ½ X 4 X √ 2
= 2 √2 cm.
Now
Consider right angle OEB
OE 2 + EB 2 = ( OB)2
OE 2+ ( 2√2) 2 = ( 6) 2
OE 2 + 4 x 2 = 36
OE 2 + 8 = 36
OE 2 = 36 – 8
OE2 = 28
OE = √28
OE = √4 x 7
OE = 2 x √ 7 cm
OE = 2 √7cm
But OE =height of the pyramid = 2√7
:.volume of square of based pyramid = 1/3 x b2 x h
1/3 x 42 x 2 x √7 cm3
1/3 x 16 x 2 x √7 cm3
= 32 x √7 cm3
3
32 x 2.646cmm3
3
= 32 x.0.882cm3
= 28. 224cm3
= 28.2cm3 to 1 d.p.
3) Since
Diameter = 14cm
Radius = diameter
2
= 14 cm.=7cm
2
:. Volume of cone = 1/3 πr2 h
= 1/3 x 22/7 x ( 7 ) 2 x 24
= 1/3 x 22/7 x 49 x 24 cm3
= 22 x 56cm3
= 1232 cm3
ASSIGNMENT
- Calculate the volume of a cylinder which has a radius of 21cm and a height of 6cm. A. 8500cm3 B. 8316cm3 C. 7632cm3 D 7500cm3 E. 8000cm3
- Calculate the total surface of the cylinder in question 1.
A, 5346cm2 B, 4653cm3 C. 3000cm2 D. 3564 cm2 E 3800cm2
- Calculate the volume of a cone which has a base diameter of 7cm and a height of 6cm A. 77cm3 B. 70cm3 C. 88cm3 D. 90cm3 E. 65cm3
- Calculate the curved surface area of the cone in question 3 above.
A, 152cm2 B. 150cm2 C. 132cm2 D 142cm2 E. 160cm2
- Calculate the total surface area of a cuboid which is 8cm by 5cm by 3cm.
A.198cm2 B. 178cm2 C 188cm2 D 168cm2 E. 158cm2.
- A water tank is 1.2m square and 1.35m deep. It is half full of water. How many times can a 9-litre bucket be filled from the tank?
- A measuring cylinder of radius 3cm contains water to a height of 49cm. If this water is poured into a similar cylinder of radius 7cm, what will be the height of the water column?
- A solid cone has a circular base of radius 7cm. the vertical height of the cone is 15cm. the cone is melted and recast into a metal cube of side xcm. Calculate correct to 3. s.f. the value of x.
- A cylindrical container with a diameter of 80cm and height 50of cm is full of liquid. The liquid is then poured into another cylinder with a diameter of 90cm. calculate the depth of the water.






















