Proof Of Some Basic Theorem And Deductive Proofs SS1 Mathematics Lesson Note
Download Lesson NoteTopic: Proof Of Some Basic Theorem And Deductive Proofs
The sum of the angles of a triangle is 180.
Given any triangle ABC
To prove: A+B+C=180°
Construction: Produce BC to a point X. Draw CP parallel to BA

Proof: Draw a triangle ABC with the following lettering:
a1=a2 (alternate angles)
b1=b2 (corresponding angles)
c+a1+b1 = 180°
C+a2+b2 = 180°
ABC + A + B = 180°
A + B + C = 180°
RELATIONSHIP TO ANGLES ON A STRAIGHT LINE
The sum of angles on a straight line is 180°.
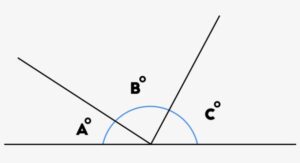
i.e. A + B + C = 180°
Angles on a parallel line cut by a transversal line:
The figure below is parallel lines cut by a transversal line indicating angles 1 – 8
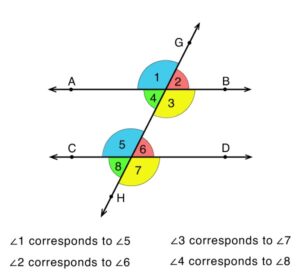
Corresponding Angles
From the figure above, the following angles are corresponding
<1 = <5 ; <3 = <7
<2 = <6 ; <4 = <8
Alternate Angles
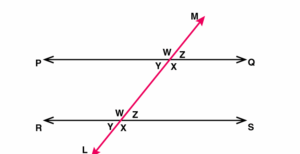
From the diagram above, the alternate angles are seen.
Vertically opposite Angles
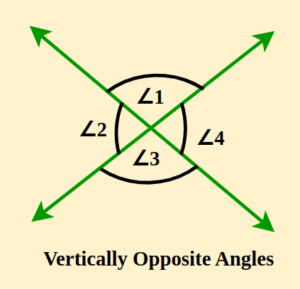
From the diagram above, the vertically opposite angles are:
<1 = <3 ; <2 = <4
PARALLELOGRAM
A parallelogram is a quadrilateral which has both pairs of opposite sides parallel.
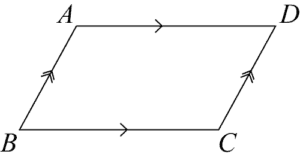
Rhombus, rectangles and squares are special examples of parallelograms. A rhombus is a parallelogram with sides of equal length.
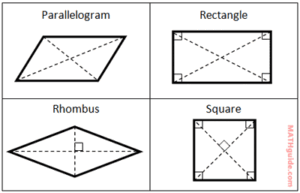
PROPERTIES OF PARALLELOGRAM
- The opposite sides are parallel.
- The opposite sides are equal.
iii. The opposite angles are equal.
- The diagonals bisect one another.
PROPERTIES OF RHOMBUS
- All four sides are equal.
- The opposite sides are parallel.
iii. The opposite angles are equal.
- The diagonals bisect one another at right angles.
- The diagonals bisect the angles.
NB: In a rectangle, all of the properties of a parallelogram are found and all four angles are right angles. In a square, all of the properties of a rhombus are found and all four angles are right angles.
INTERCEPT THEOREM
If three or more parallel lines cut off equal intercepts on a transversal, then they cut off equal intercepts on any other transversal.
Given: Three parallel lines cutting a fourth line at A, B, and C so that /AB/=/BC/ and cutting another line at X, Y, and Z respectively.
To prove:/XY/ = /YZ/.
Construction: Draw XP and YQ parallel to ABC to cut BY and CZ at P and Q respectively.
Proof:
AXPB is a parallelogram (opp. Sides //)
XP = AB (opp side equal)
Similarly /YQ/ = /BC/ (in //gm YQCB)
/XP/ = /YQ/ (given AB = BC )
In triangles XPY, YQZ
/XP/ =/YQ/ (Proved)
X1 = x2 (corr. angles)
Y1 = y2 (corr. angles)
Therefore, triangle XPY = triangle YQZ (AAS)
/XY/ = /YZ/
ASSIGNMENT
- In triangle ABC, <BAC= 68o and <ABC = 30o. BC is produced to X. The bisectors of <ABC and <ACX meet at P. calculate <BCP and <BPC.






















