Area Of Sector And Segment SS1 Mathematics Lesson Note
Download Lesson NoteTopic: Area Of Sector And Segment
AREA OF SECTORS
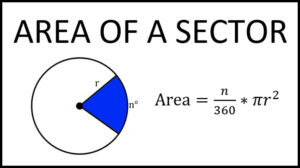
The area of a sector of a circle is given by the formula;
Area of sector = θ x πr 2 ÷ 360°
where r = radius of the circle, θ = angle subtended at the centre by XY or angle of the sector
Examples
Calculate the area of a sector of a circle which subtends an angle of 45° at the centre of the circle, diameter 28cm (π = 22/7).
The area of a circle PQR with centre O is 72cm2. What is the area of sector POQ, if POQ = 40°?
Solutions
- Since the diameter of the circle = 28cm
d = 2r = 28
where d = diameter and r = radius
thus 2r = 28
2r = 28 = 14cm
2
Area of sector = θ x πr 2 ÷ 360°
= 45 x 22 x ( 14 ) 2
360 7
= 1/8 x 22/7 x 14 x 14 cm
= 77cm2
- Since the area of the whole circle PQR = 72cm2
Then
Area of sector = θ x πr2 ÷ 360°
But πr2= Area of the whole circle PQR = 72cm2
:. Area of = 40 x 72cm2
sector POQ ÷ 360°
= 8cm2
AREA OF SEGMENTS
A segment of a circle is the area bounded by a chord and an arc of the circle. Considering the figure below, we have a major segment and a minor segment.
In a diagram, the Area of the shaded segment= Area of sector POQ – Area of triangle POQ = θ
360° x πr2 – ½ r2 sin θ
Where
r = radius of the circle
θ = angle subtended by the sector at the centre
Π= a constant = 22/7
ASSIGNMENT
- Calculate the area of a sector of a circle of radius 6cm which subtends an angle of 70° at the centre (π = 22/7) A. 44cm2 B. 22cm2 C. 66cm2 D. 11cm2 E. 16.5cm2
- What is the angle subtended at the centre of a sector of a circle of radius 2cm if the area of the sector is 2.2 cm2? (π = 22/7)A. 120° B. 31 ½° C. 43° D. 58° E. 63°
- What is the radius of a sector of a circle which subtends 140° at its centre and has an area of 99 m2? A 18m B. 27m C. 9m E. 30m E. 24m
- A sector of 80° is removed from a circle of radius 12cm What area of the circle is left? A. 253cm2 B. 704cm2C 176cm2D. 125cm2 E. 352cm2π






















