Gravitational Field SS1 Further Mathematics Lesson Note

INTRODUCTION

A gravitational field is a region or space around a mass in which the gravitational force of the mass can be felt. Gravitation is the force of attraction exerted by a body on all other bodies in the universe. 

Gravitational force acts between all masses and holds together planets, stars and galaxies.  Each mass has a gravitational field around it.

Law Of Universal Gravitation 

Newton’s law of universal gravitation states that every particle in the universe attracts every other particle with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between them

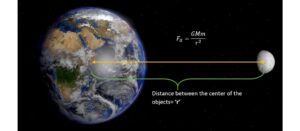
The law can be expressed mathematically as:

F ά M1M2 ………………… 1

F ά 1 ÷ r2 ……………………2

F ά M1M2 ……………………3

        r2

:. F = G M1M2 ……………………4

              r2

M1 and M2 are the masses of the two particles r is the distance between them and G is the universal gravitational constant.  The numerical value of G = 6.67 x 10-11 Nm2 kg -2.

Gravitational Field Intensity

Gravitational field intensity at a point is the force per unit mass of an object placed at that point.

g = F ÷ M

The unit is N/Kg. It is a vector quantity and it is regarded as acceleration due to gravity.

Relation between g and G

If the force of attraction (F) between two particles of matter separated by a distance r is given by:

F = GMm…………………..1

        R2

But g = F ÷ m    …………………2

:. g = GMm   x 1

   r2     m

 g= GM ÷ r2 …………3

This is the gravitational intensity 

Gravitational Potential 

The gravitational potential at a point is the work done in taking a unit mass from infinity to that point. The unit is Jkg-1.

The gravitational potential, V, is given by

V = Gm ÷ r

m is the mass producing the gravitational field and r is the distance of the point to the mass.  

The gravitational potential decreases as r increases and becomes zero when r is infinitely large. The negative sign indicates that the potential at infinity (zero) is higher than the potential close to the mass.

Escape Velocity 

This is the minimum velocity required for an object (e.g. satellite, rocket) to just escape or leave the gravitational influence or field of an astronomical body (e.g. the earth) permanently.

M(e)= mass of the earth, m = mass of the satellite

Then F = GM(e)m ÷ r2

The work done in carrying a mass m from a point at a distance r from the centre of the earth to a distance so great is

W = GMm  x r

               r2

This work must equal the Kinetic energy of the body of mass m at this point, having a velocity, of Ve

Thus KE = ½ mV2

:. 1/2mVe2 = GMem x r

                          r2

If the mass was launched from the earth’s surface where r = R.

Then Ve2 = 2GMe

                          R

Ve2 = 2Gm x R

            R2

But g =  Gm

               R2

Ve2 = 2gR

Ve2 = √2gR

Energy in Gravitational Field

 A satellite moving in an orbit around the Earth has both kinetic and potential energy

The centripetal force 

= mv2 = GMm

     r2       r2

KE = ½ mv2 = GMm

                          r

PE of mass in orbit   = – GMm

                                            r

The total energy in orbit = PE + KE

       = – GMm + GMm

                r         2r

= GMm

                               2r

The following conclusions can be drawn from the equation.

1. The magnitude of the total energy is equal to that of the k.e of the satellite.
2. The kinetic energy of a satellite in an orbit increases as the radius of the orbit decreases.

iii. The kinetic energy of a satellite in an orbit increases as the speed of the satellite increases.

1. The potential energy of the satellite in orbit is twice its kinetic energy and of opposite sign.

ASSIGNMENT 

1. State Newton’s law of universal gravitation and give the mathematical relation
2. Calculate the gravitational potential at a point on the Earth’s surface. Mass of earth is 6.0x 10 24 /kg, radius of earth = 6400km and G = 6.67×10 -11Nm2kg-2
3. Calculate the escape velocity of a satellite from the earth’s gravitational field (g = 9.8m/s2, R = 6.4 x 10 6m)
4. What is escape velocity?