Sets II – Operation of Set & Venn Diagrams SS1 Further Mathematics Lesson Note

OPERATION OF SET AND VENN DIAGRAMS

Using Venn diagrams to solve problems involving three sets

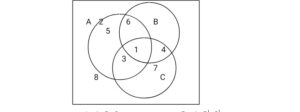
1= AnBnC      5 = AnBInCI

2 = AnBnCI 6 = A1nBnC1l

3 = AnBInC 7 = A1nBInC

4 = AInBnC 8 = (AnBnC)1

Example: A school has 37 vacancies for teachers, out of which 22 are for English, 20 for History and 17 for Fine Art. Of these vacancies 11 are for both English and History, 8 for both History and Fine Art and 7 for English and Fine Art. Using a Venn diagram, find the number of teachers who must be able to teach:

(a.) all the three subjects

(b.) Fine Art only

(c.) English and History but not Fine Art.

Solution:

Let µ = {All vacancies for teachers}

      E = {English vacancies}

      H = {History vacancies}

      F = {Fine Art vacancies}

µ = 37, n(E)= 22, n(H)= 20, n(F)= 17, n{EnH}= 11, n(HnF)= 8, n(EnF)= 7

Let n(EnFnH) = y

n (EnHInF)= n(E)- (7-y+y+11-y)

= 22- (18-y)            =   4 + y

n(EInHnF) = n(H)  (11-y+y+8-y)

= 20- (19-y)          =    1+y

n(EInH1nF)= n(F)  ( 7-y +y+8-y)

= 17  (15- y)        =   2 +y

µ= 4+y+11-y+1+y+y+8-y+7-y+2+y

37= 33 + y

y = 37- 33

y = 4.                

n(EnHnF) = 4 teachers

(2.)    Fine Art only, n(EInHInF) = 2+ y

= 2+4    = 6 teachers

(3.)    English and History but not Fine Art i.e English and History only

n(EnHnFI) = 11-y

= 11- 4 = 7 teachers.

ASSIGNMENT 

1. At a meeting of 35 teachers, the analysis of how Fanta, Coke and Pepsi were served as refreshments is as follows. 15 drank Fanta, 6 drank both Fanta and Coke, 18 drank Coke, 8 drank both Coke and Pepsi, 20 drank Pepsi, and 2 drank all three types of drink. How many of the teachers drank:
2. Coke only 
3. Fanta and Pepsi but not Coke. 
4. Given n(XUY) = 50, n(X) = 20 and n(Y) = 40, determine n(XnY)