Sets SS1 Further Mathematics Lesson Note

IDEA OF SET, NOTATIONS, APPLICATIONS.

Definitions:

A set can be defined as a group or a collection of well-defined objects or numbers e.g. collection of books, or cooking utensils.

A set is denoted by capital letters such as P, Q, and R e.t.c while small letters are used to denote the elements e.g. a, b, c

Common Terms Used 

1. Elements of a set: These are the elements or members of a given set. The elements are separated by commas and enclosed by a curly bracket {}

e.g M ={ 1, 3 ,5, 7, 11}, 1  is an element of M.

Example: Write down the elements in each of the following sets.

A = {Odd numbers from 1 to 21}

F = {factors of 30}

M = {Multiples of 4 up to 40}

Solution:

A  = { 1,3,5,7,9,11,13,15,17,19,21}

F = {1, 3, 5, 6, 10, 15, 30}

M = {4, 8, 12, 16, 20, 24, 28, 32, 36, 40}

2. Cardinality of a set: This is the number of elements in a set.

Example: Given that µ= {all the days of the week}, B= {all days of the week whose letter begin with s}

1. a) List all the elements of µ
2. b) List the members of B
3. c) What is n (µ)                  
4. d) What is n(µ) + n(B)

Solution:

1. a) µ = {Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday}
2. b) B = {Sunday, Saturday}
3. c) n (µ) = 7
4. d) n (µ) + n(B) = 7 + 2= 9

3. Set notation: A set can be described algebraically using inequality and other symbols. E.g B = {x: -10≤x ≤ 3, x is an integer}

Example: List the members of the following sets 

1. A= {x: 5< x< 8}
2. B= {x: 0≤ x≤ 5}

Solution;

1. A = {6, 7}
2. B = {0, 1, 2, 3, 4, 5}

Types of Sets:

Finite and Infinite set

1. A finite set is a set in which all its members can be listed.

2. Infinite set: An infinite set is a set in which all its members cannot be listed.
3. Empty (Null) set: A set without any member. It is usually denoted by { } or Ø.
4. Subset and Supersets: If we have 2 sets A and B such that all the elements in A are contained in B, then A is a subset of B. Subset is denoted by C e.g. A C B. If there is at least one element in set B but not in A, then B is a superset of A.
5. Disjoint set: Two sets are disjoint when there is no common element between them. i.e. no intersection.

A n B = Ø                                                                                                          6. Universal set: This is a set that contains all the members under consideration for any given problem. It is denoted by µ or €.

7. Complementary Set: This is a set that contains the members in the universal set that are not in set A. It is denoted by Ac or A1.

Other Terms Used In Sets

1. Intersection of sets: This is the set which consists of all the common elements in a given two or more sets. It is denoted by n.
2. Union of sets: This is the set of all members that belong to A or B or both A and B. It is denoted by u.

Example: If the universal set µ= {x: 1≤ x ≤ 12} and its subsets D, F and G are given as follows. D = {x: 2<x<8}, F={x: 4≤ x≤ 10}, G={x: 1< x ≤ 4}

Find:

(a) D U F

(b) D n F

(c) G1

(d) (D n G)1

Solution: 

µ   = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

D = {3, 4, 5, 6, 7}

F   = {4, 5, 6, 7, 8, 9, 10}

G = {2, 3, 4}

1. a) D U F ={ 3, 4, 5, 6, 7,8, 9,10}
2. b) DnF = {4, 5, 6, 7}
3. c) G1     = { 1, 5, 6, 7, 8,9,10,11,12]
4. d) i. (D n G)1  
5. D n G = {3, 4}

iii. (D n G)1 = {1, 2, 5, 6, 7,8, 9,10,11,12}

Relationship Between Union and Intersection Of Sets

n(A or B)  = n( A) + n( B) n( A and B)\  

  or   n(AUB)     = n(A) + n( B)  – n(A n B)

Example:

If n(A)=23, n(B)= 12, n( AUB) = 35, find  n(AnB) and comment on set A and B.

Solution

n(AUB) = n( A) + n( B)  n(AnB)

= 23 + 12 n(AnB)

      n(AnB) = 35- 35

      n (AnB) = 0

Set A and B are disjoint.

Venn Diagrams:

The Venn diagram is a geometric representation of sets using diagrams which show different relationships between two or more sets. In order words, it is the diagrammatical representation of relationships between two or more sets. The operations of intersection, union and complementation of sets can be demonstrated by using Venn diagrams.

Use of Venn Diagrams To Solve Problems Involving Two Sets

Examples:

1. Out of the 400 final-year students in a secondary school, 300 are offering Biology and 190 are offering Chemistry. If only 70 students are offering neither Biology nor Chemistry. How many students are offering: 

(i)  both Biology and Chemistry? 

(ii) At least one of Biology or Chemistry?

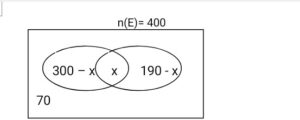
Let the number of students who offered both Biology and Chemistry be X i.e (BC)= X. from the information given in the question

n(E)= 400

n(B)= 300

n(C)= 190

n(BƲC)|=  70

since the sum of the number of elements in all regions is equal to the total number of elements in the universal sets, then:

300 – x  + x +190 – x + 70 =400

560 – x= 400

-x= 400  560

X= 160

The number of students offers both Biology and Chemistry= 160

(ii)no of students offering at least one of biology and chemistry from the Venn diagram this includes those who offered biology only, chemistry only and those who offered both i.e 

300 – x + 190 – x + x= 490

490 – 160 (from (i) above)=  330

2. In a youth club with 90 members, 60 like modern music and 50 like traditional music. The members of them who like both traditional and modern music are three times those who do not like any type of music. How many members like only one type of music

Solution

Let the members who do not like any type of music = X

Then,

n(TnM)= 3X

Also,

n(E)= 94

n(M)=60

n(T)= 50

n(MƲT)|= X

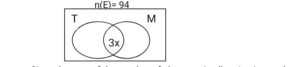
Since the sum of the number of elements in all regions is equal to the total number of elements in the universal set, then

60 – 3X + 3X + 50 – 3X = 94

110 – 2X= 94

16= 2X

Divide both sides by 2

16= 2X

2     2

X= 8

Therefore number of members who like only one type of music are those who like modern music only  + those who like traditional music only

60 -3x  + 3X + 50  3X= 110

110 – 6 x 8 (from above)

= 110  48

= 62

Two Venn Diagrams 

Where 1 = AnBI , 2 = AnB, 3 = AInB, 4 = ( AUB)I

Therefore, µ = 1 + 2 + 3 + 4

µ = n( AnBI) + n( AnB) + n( AInB) + n( AUB)I

Example 1: In a class of 40 students, every student had to study French Russian or both subjects. 25 students studied French and 20 studied Russian. Find the number of students who studied both languages.

Solution:

Let µ = {All the students}

F = {French students}, R = {Students studying Russian}

µ = 40, n(F)= 25, n(R) = 20

n( Fn R)= x

n(FnRI) = 25-x                                                                                                                                     

n (Rn FI)= 20- x

µ = 25 x +x + 20-x

40= 45 – x

x = 45 – 40

x=5,  n(FnR) = 5 students.

ASSIGNMENT 

1. In a senior secondary school, 90 students play hockey or football. The number that play football is 5 more than twice the number that play hockey. If 5 students play both games and every student in the school plays at least one of the games. Find:
2. The number of students that play football
3. The number of students that play football but not hockey

iii. The number of students that play hockey but  not football

2. A, B and C are subsets of the universal set U such that

U={0,1,2,3,4………….12}

A={X: 0≤X7}        B= {4,6,8,10,12}        C= {1<y<8} where Y is a prime number.

1. Draw a Venn diagram to illustrate the information

Find (a) BƲC (b) AB∩C