Angles And Polygons JSS2 Mathematics Lesson Note
Download Lesson NoteTopic: Angles And Polygons
ANGLES AND POLYGON
TYPES AND PROPERTIES OF ANGLES
Straight Angles
Angles which measure exactly 180° (degrees) are straight. Therefore, straight angles are straight lines. Angles are represented by the sign ϴ, called theta. That is, for straight angles, ϴ= 180°.

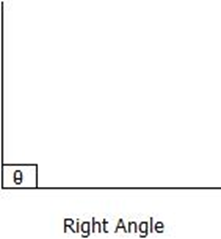
Right Angles
Angles which measure exactly 90° are right angles, that is, ϴ = 90°.
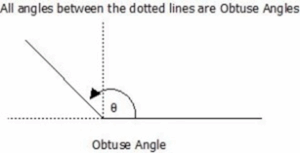
Obtuse Angles
Obtuse angles are those which are greater than 90° but less than 180°, that is, 90° < ϴ < 180°.
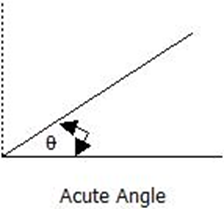
Acute Angles
Acute angles are angles that are greater than 0° but less than 90°, that is, 0° < ϴ < 90°.
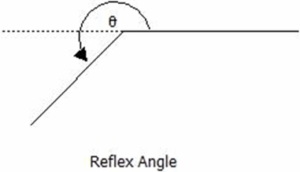
Reflex Angles
Reflex angles are angles that are greater than 180° but less than 360°, that is, 180° < ϴ < 360°.
Adjacent Angles
Two angles that share the same vertex (center, usually represented by 0) and have a common side (line) are called adjacent angles.
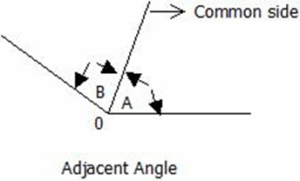
Complementary Angles
Complementary angles are two angles which when summed equals 90°.
Note: <A and <B, are ‘angle A’ and ‘angle B’ respectively.

Supplementary Angles
Supplementary angles are two angles which when summed equals 180°.
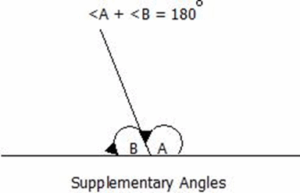
Vertically Opposite Angles
Vertically opposite angles are the angles opposite to each other when two straight lines intersect. Their defining property is that vertically opposite angles are equal in magnitude.
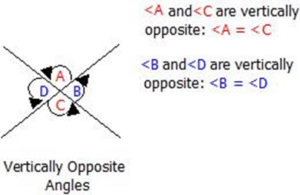
Corresponding Angles
When two parallel lines are crossed by a line called the transversal, the angles formed which are in corresponding positions, are called corresponding angles. Corresponding angles are equal in magnitude.
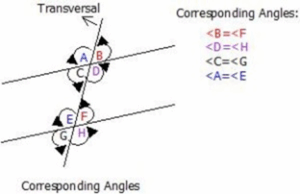
POLYGON: A part of a triangle and quadrilateral, we have other polygons which are also named according to the number of sides they have.
Examples are pentagon = 5, Hexagon = 6. It can be regular or irregular. A polygon is said to be regular when all the sides and angles are equal. An irregular polygon has neither of the sides or angles equal.
TYPES OF POLYGON (Regular Polygons)
Regular polygons have all sides, and all angles equal.

Size of Internal Angles
To find the size of the internal angles of a regular polygon with ‘n’ sides, use the formula:
For example, the size of the interior angles of the pentagon (five sides) above is:
The sum of all the interior angles of a polygon with ‘n’ sides is found using the formula:
(n – 2) x 180°
Therefore, the sum of all the interior angles of the pentagon above is:
(5 – 2) x 180° = 3 x 180° = 540°
Size of Exterior Angles
Interior and Exterior angles are measured on the same line, that is, they add up to 180°.
Therefore, the size of an exterior angle = 180° – Interior angle.
For example, the size of the external angle of the pentagon above is:
Since, interior angle = 108°
Then, exterior angle = 180° – Interior angle
180° – 108° = 72°
Below is a list of the names and the number of sides, of some of the most popular polygons.
| Name of Polygon | Number of Sides |
| Equilateral Triangle | 3 |
| Quadrilateral | 4 |
| Pentagon | 5 |
| Hexagon | 6 |
| Heptagon | 7 |
| Octagon | 8 |
| Nonagon | 9 |
| Decagon | 10 |
DO THESE:
- Calculate the total internal angle of an octagon
- The size of each angle of a regular octagon
- The total internal of a decagon
- The size of each angle of a regular decagon.






















