Three Dimensional Shapes JSS1 Mathematics Lesson Note

THREE-DIMENSIONAL SHAPES

Solid figures are often called 3-dimensional shapes. A solid figure is simply anything that occupies space and also has a definite shape.

FACES, EDGES AND VERTICES

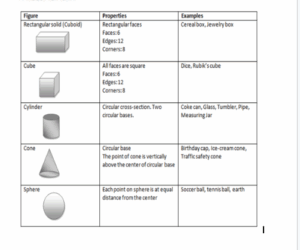
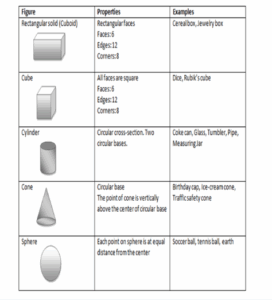
FACE: A face is the surface of a solid which is enclosed by edges.

EDGES: An edge of a solid is a line where two faces meet. Note that an edge may be straight or curved

VERTEX: A vertex of a solid is a point or corner where three or more edges meet.

TYPES OF SOLID AND THEIR PROPERTIES 

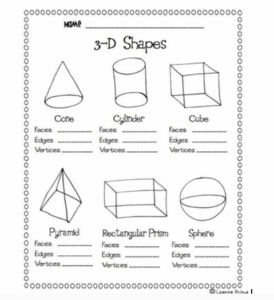
DO THESE

APPLICATION

Surface Area

The surface area of a figure is the total area of all the sides of the figure.

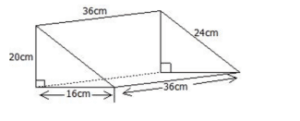
Triangular Prism (Right Angle Triangle)

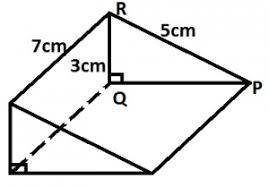
To find the surface area of the prism above, follow the steps below.

Step 1:       Divide the figure into smaller shapes.

Step 2:       Find the area of each smaller shape.

Step 3:       Add the areas of each smaller shape.

A right-angle triangle prism can be divided into five smaller shapes: two right-angle triangles and three rectangles.

Example

Find the surface area of the prism below.

Pyramid

A pyramid is an object that has a straight-sided shape base (a square, rectangular, or triangular base, etc) and triangular sides that meet at the top (called the apex).

 Example

Cylinder

To find the surface area of the cylinder above, follow the steps below.

Step 1: Divide the figure into smaller shapes.

Step 2: Find the area of each smaller shape.

Step 3: Add the areas of each smaller shape.

A cylinder can be divided into three segments: two circles and a curved surface area.

The area of a circle is A = πr².

Since there are two circles in a cylinder, multiply the above formula by 2, that is:

The area of the circles is A = 2πr2

The curved surface area, C.S.A. = 2πrh

The area of a cylinder, A = Area of the circles + C.S.A.

                                                  = 2πr2 + 2πrh

                                                  = 2πr (r + h)

Example

Cube

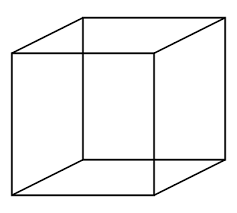
A cube has 6 sides (faces) of the same surface area. Each side (face) of the cube is square. Recall, the area of a square, A = L2.

The surface area of a cube is A = 6L2

Where L is the length of a side of the cube (all the sides of a cube are the same length).

Example

Cuboid

The surface area of a cuboid is A =  2Lw + 2Lh+ 2wh

Where L is the length of the cuboid

w is the width of the cuboid

And h is the height of the cuboid

Sphere

A sphere is a three-dimensional object (such as a ball or the earth) with every point on the surface equidistant (halfway from) from the center.

The surface area of a sphere is A = 4πr².

Where r is the radius of the sphere.

Surface Area of a sphere, A = 4πr²