Identification & Properties of Angles JSS1 Mathematics Lesson Note

 IDENTIFICATION AND PROPERTIES OF ANGLES

TYPES AND PROPERTIES OF ANGLES

Straight Angles

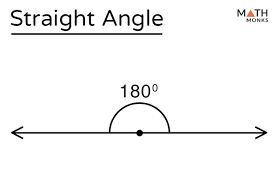
Angles that measure exactly 180° (degrees) are straight. Therefore, straight angles are straight lines. Angles are represented by the sign ϴ, called theta. That is, for straight angles, ϴ = 180°.

Right Angles

Angles which measure exactly 90° are right angles, that is, ϴ = 90°.

Obtuse Angles 

Obtuse angles are those which are greater than 90° but less than 180°, that is, 90° < ϴ < 180°.

Acute Angles 

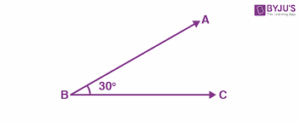
Acute angles are angles that are greater than 0° but less than 90°, that is, 0° < ϴ < 90°.

Reflex Angles

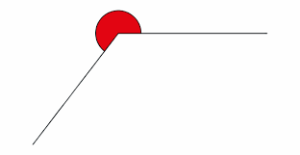
Reflex angles are angles that are greater than 180° but less than 360°, that is, 180° <ϴ< 360°.

Adjacent Angles

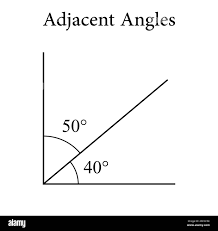
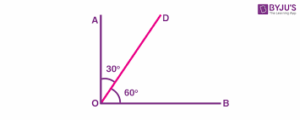
Two angles that share the same vertex (center, usually represented by 0) and have a common side (line) are called adjacent angles.

Complementary Angles

Complementary angles are two angles that, when summed, equal 90°.

Note: <A and <B are ‘angle A’ and ‘angle B’ respectively.

Supplementary Angles

Supplementary angles are two angles that when summed, equal 180°.

Vertically Opposite Angles

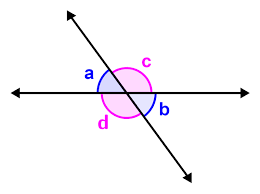
Vertically opposite angles are the angles opposite to each other when two straight lines intersect. Their defining property is that vertically opposite angles are equal in magnitude.

Corresponding Angles

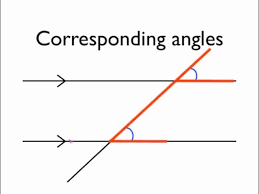
When two parallel lines are crossed by a line called the transversal, the angles formed, which are in corresponding positions, are called corresponding angles. Corresponding angles are equal in magnitude.

Obtuse-Angled Triangles

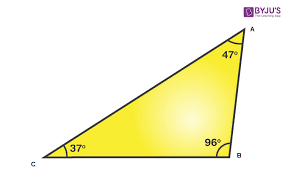
Obtuse-angled triangles are triangles with one of their angles greater than 90° but less than 180° (i.e. an obtuse angle).

Acute-Angled Triangles

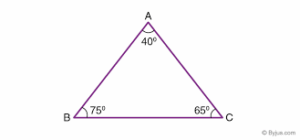
Acute-angled triangles are triangles in which all the angles are acute. That is, all angles are greater than 0° but less than 90°.