Conic Sections SS3 Further Mathematics Lesson Note

SPECIFIC OBJECTIVES: At the end of the lesson, students should be able to recognize the two-dimensional equations of; 

1. A parabola; 
2. An ellipse; 
3. A hyperbola and;
4. Able to solve problems on a parabola, an ellipse and a hyperbola

INSTRUCTIONAL RESOURCES: 

• The solid shapes of parabolic, 
• elliptic and hyperbolic types etc. 

LESSON PRESENTATION: The teacher presents the lesson step by step by first asking the students questions based on previous lessons, for example, what is a circle? Etc. 

STEP 1 

MODE: ENTIRE CLASS Identification of prior ideal, for example, the teacher arouses students’ interest by asking them questions relevant to the lesson, for example, what is a circle? Etc. 

TEACHER’S ACTIVITIES 

THE PARABOLA 

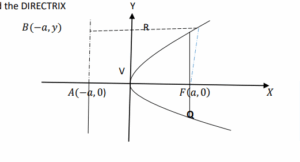
Definition: A parabola is a locus of points equidistant from a given point, called the DIRECTRIX and from a given line called the DIRECTRIX 

From the diagram above, line AB a distance of a from the y-axis is called the DIRECTRIX, line AF is called the AXIS OF SYMMETRY, point V is called the VERTEX, the line with endpoints R and Q is called the LATUS RECTUM EQUATION OF THE PARABOLA The equation of the parabola is 𝑦 2 = 4𝑎x

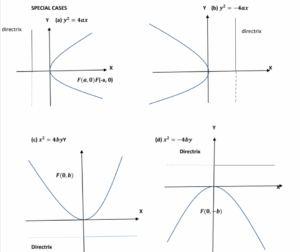
Directrix If the vertex of the parabola 𝑦 2 = 4𝑎𝑥is translated to the point (𝑥1, 𝑦1), the equation of the corresponding parabola becomes (𝑦 − 𝑦1) 2 = 4𝑎(𝑥 − 𝑥1) The above equation is said to be in the standard or canonical form 

Example: 1 

Find the focus and directrix of the parabola 𝑦 2 = 16𝑥 directrix directrix 

Solution 

By comparing 𝑦 2 = 16𝑥 𝑤𝑖𝑡ℎ 𝑦 2 = 4𝑎𝑥 4𝑎 = 16 𝑎 = 4 

Hence, the focus is (4,0) While the directrix is 𝑥 = −4 

Example: 2. 

Write the equation 𝑦 2 − 4𝑦 − 12𝑥 + 40 = 0 in canonical form and hence determine vertex, focus and directrix 

Solution 

𝑦 2 − 4𝑦 − 12𝑥 + 40 = 0 𝑦 2 − 4𝑦 + 4 − 12𝑥 + 36 = 0 𝑦 2 − 4𝑦 + 4 = 12𝑥 − 36 (𝑦 − 2) 2 = 12(𝑥 − 3) 

Hence, the vertex is (3, 2) 

Since 4𝑎 = 12 ⇒ 𝑎 = 3, 

The focus is (3 + 3, 2) = (6,2) 

The directrix is 𝑥 = 3 − 3 = 0 

Example 3: 

Find the equation of the parabola whose vertices are the origin and whose focus is the point 𝐹(5,0) 

Solution 

Let the equation of the parabola be 𝑦 2 = 4𝑎𝑥 

The focus 𝐹(𝑎, 0) = (5,0) ∴ 𝑎 = 5 

Hence, the equation of the parabola is 𝑦 2 = 20𝑥 

STUDENTS ACTIVITIES 

1. Find the foci and directories of the following parabola; (a) 𝑦 2 = 32𝑥 𝐴𝑛𝑠. 𝐹𝑜𝑐𝑢𝑠 (8,0) 𝑑𝑖𝑟𝑒𝑐𝑡𝑟𝑖𝑥 𝑥 = −8 (b) 𝑦 2 = −40𝑥 𝐴𝑛𝑠. 𝐹𝑜𝑐𝑢𝑠 (−10,0) 𝑑𝑖𝑟𝑒𝑐𝑡𝑟𝑖𝑥 𝑥 = 10 (c) 𝑥 2 = 12𝑦 𝐴𝑛𝑠. 𝐹𝑜𝑐𝑢𝑠 (0,3) 𝑑𝑖𝑟𝑒𝑐𝑡𝑟𝑖𝑥 𝑦 = −3 (d) 𝑥 2 = −50𝑦 𝐴𝑛𝑠. 𝐹𝑜𝑐𝑢𝑠 (0, − 25 2 ) 𝑑𝑖𝑟𝑒𝑐𝑡𝑟𝑖𝑥 𝑦 = 25 2 
2. Write the equations of the following parabola in their canonical form and hence determine their vertices, foci and directories (a) 𝑦 2 − 6𝑦 − 2𝑥 + 19 = 0 𝐴𝑛𝑠. (𝑦 − 3) 2 = 2(𝑥 − 5), 𝑉(5,3), 𝐹 ( 11 2 , 3) 𝑎𝑛𝑑 𝑥 = 9 2 (b) 𝑦 2 + 4𝑦 + 4𝑥 + 16 = 0 𝐴𝑛𝑠. (𝑦 + 2) 2 = −4(𝑥 + 3), 𝑉(−3, −2), 𝐹(−4, −2)𝑎𝑛𝑑 𝑥 = −2 (c) 𝑥 2 − 6𝑥 − 4𝑦 + 13 = 0 𝐴𝑛𝑠. (𝑥 − 3) 2 = 4(𝑦 − 1), 𝑉(3,1), 𝐹(3,2)𝑎𝑛𝑑 𝑦 = 0 (d) 𝑥 2 + 4𝑥 + 4𝑦 + 16 = 0 𝐴𝑛𝑠. (𝑥 + 2) 2 = −4(𝑦 + 3), 𝑉(−2, −3), 𝐹(−2, −4)𝑎𝑛𝑑 𝑦 = −2 
3. Find the equations of the following parabola whose vertices is the origin and whose foci are the points (𝑎) 𝐹(−4,0)(𝑏) 𝐹(0,5)(𝑐) 𝐹(0, −4)