Chords Properties Of Circle SS2 Mathematics Lesson Note

INTRODUCTION OF A CIRCLE AND IT’S PROPERTIES

i. Parts Of A Circle: 

– The centre is the point in the middle of a circle. 

– The circumference is the curved outer boundary of the circle. 

– An arc is a curved part of the circumference. 

– A radius is any straight line joining the centre to the circumference. The plural of radius is radii.

– A chord is any straight line joining two points on the circumference. 

– A diameter is a straight line which divides the circle into two equal parts or a diameter is any chord which goes through the centre of the circle.

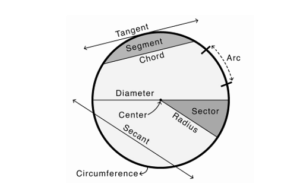
ii. Region Of A Circle

– A sector is the region between two radii and the circumference. 

– A semi-circle is a region between a diameter and the circumference i.e. half of the circle. 

– A segment is the region between a chord and the circumference.

CALCULATION OF THE LENGTH OF THE ARC AND PERIMETER OF A SECTOR 

Given a circle centre O with radius r. The circumference of the circle is 2Пr. Therefore, the length, L, of arc XY is given as L =   θ x  2Пr ÷ 360°

Where θ is the angle subtended at the centre by arc XY and r is the radius of the circle.

 Also,

The perimeter of Sector XOY = r + r + L

Where L = length of arc XY 

= θ     X    2 Пr ÷ 360

 Then Perimeter of Sector XOY 

=r  +  r  + L

= 2r  +   θ     x    2 Пr ÷ 360°

EXAMPLES

1. An arc of length 28cm subtends an angle of 240°  at the centre of a circle. In the same circle, what angle does an arc of length 35cm subtend?
2.  Calculate the perimeter of a sector of a circle of radius 7cm, the angle of the sector being 108°, if П is 22/7.

Solutions:

1. L =    θ   x    2 Пr ÷ 360°

When L = 28cm ,  θ =  240, r = ?       

Then    L =  θ    x    2 Пr ÷ 360°

 28 = 24   x    2 x (22 ÷ 7)  x r   ÷   360°            

Cross-multiply:

24  x  44 x r  =  28 x  360 x  7

15.                 7         60

r = 28  x  360  x  7 cm

              24×44

       4         11

 r  =  49  x   15  cm

                11

r = 735 cm

      11

Also 

When L = 35cm, r = 735 cm

                                     11

θ  = ?

 Then 

L =  θ   x  2 Пr

           360°

 35 = θ   x 2  x  22  x  735

      360              7        11

 Then,

Cross multiply

x  360 x 7 x 11 = θ x 44 x 735

   1                                  11

35 x 360 x 77    =  θ

 44     x       735

   4        105  3

 360    =   θ  = 30°

12

Thus, when the length of the arc is 35cm, the angle subtended at the centre is 30°

2. Perimeter of a sector of a circle = 2r + θ   x 2 Пr ÷ 360°

=  2 x 7 + 108   x 2 x 22 x 7

            360             7  1

          3

= 14 +  108  x  44cm

    360 10

= 14 + 3 x 44 cm

              10

=  14 + 132 cm

             10 

=  14 + 13.2 cm

= 27.2 cm

Length of chord and perimeter of a segment.

Consider a circle centre O with radius r. If OC is the perpendicular distance from O to chord AB and angle AOB = 2θ, then the length of chord AB can be found as follows: In a right-angled triangle OCA

 AC    =    Sin  θ

  r

Cross multiply:

__

AC = r Sin θ

Since

AB  = 2  x AC

AB    =  2r  Sin θ

 Where

r = radius of the circle

θ =Semi Vertical angle of the sector i.e. half of the angle subtended at the centre by arc AB.

Also

The perimeter of segment ACBD    = Length of chord AB + length of arc ADB

= 2r Sin θ + θ   x 2 Пr

    360°

Example

1. In a circle of radius 6 cm, a chord is drawn 3cm from the centre. 

(a) Calculate the angle subtended by the chord at the centre of the circle.

 (b) Find the length of the minor arc cut off by the chord

Solutions:

1. a) Let the required angle 

    = AOB = 2θ

Where

θ  = Semi-vertical angle of the sector.

 Then

Cos θ = 3cm = 1

              6cm    2

 Cos θ = 0.5000

    θ = Cos-1  0.5000

    θ   = 60°

-: Required angle = 2θ

             = 2 x 60°

            = 120°

 b) Length of minor arc ADB =θ x 2 Пr

     1           2               360°

= 120 x 2 x 22 x 6cm

360       7

3

     1

= 4 x 22cm

       7

= 88cm = 12 4cm

     7               7

ASSIGNMENT 

1. Calculate the  area of a sector of a circle of radius 6cm which subtends an angle of 70° at the centre (π = 22/7)     A. 44cm2        B. 22cm2        C. 66cm2   D. 11cm2   E. 16.5cm2

2. What is the angle subtended at the centre of a sector of a circle of radius 2cm if the area of the sector is 2.2 cm2? (π = 22/7) A. 120°    B. 31 ½°   C. 43° D. 58°   E. 63°

3. What is the radius of a sector of a circle which subtends 140o at its centre and has an area of 99 m2? A.  18m        27m        C 9m        E. 30m        E. 24m

4. A sector of 80° is removed from a circle of radius 12cm What area of the circle is left?  A. 253cm2   B. 704cm2C 176cm2D. 125cm2 E. 352cm2π

5. An arc of a circle radius 7cm is 14cm long. What angle does the arc subtend at the centre of the circle?

6. An arc of a circle whose radius is 10cm subtends an angle of 600 at the centre. Find the length of the arc.