Gas Law SS1 Chemistry Lesson Note

BOYLE’S LAW

It states that the volume of a fixed mass of gas is inversely proportional to the pressure provided the temperature remains constant.

Mathematically,

    V α 1/P

    V = k/P

    PV = k

Hence, P1V1 = P2V2

Boyle’s law can be represented graphically as shown below.

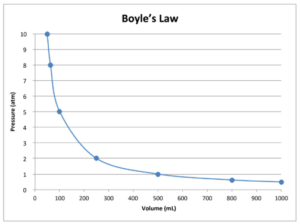
The graph shows that if the pressure is doubled, the volume is reduced to half its former value and if it is halved, the volume is doubled.

EXPLANATION OF BOYLE’S LAW USING THE KINETIC THEORY

When the volume of fixed mass of gas is decreased, the molecules of the gas will collide with each other more rapidly. This gives rise to an increase in pressure. However, if molecules are farther apart the number of collisions for unit time decreases, resulting in a decrease in pressure.

CHARLES’ LAW

Charles’ law states that the volume of a fixed mass of gas at constant pressure is directly proportional to its temperature in the Kelvin scale.

Mathematically,

   V α T

   V = k/T

V = k    T

Hence,   V1 = V2

  T1   T2

The graphical representation of Charles’ law is as shown below:

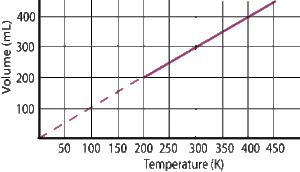
EXPLANATION OF CHARLES’ LAW USING THE KINETIC THEORY

When a given gas is heated at constant pressure, the molecules acquire more kinetic energy and move faster. They collide with one another and with the walls of the container more frequently. To maintain the same number of collisions on the walls of the container (i.e. keep the pressure constant) the volume of the gas increases.

CALCULATIONS BASED ON BOYLE’S AND CHARLES’ LAW

1. 200cm3 of a gas has a pressure of 510mmHg. What will be its volume if the pressure is increased to 780mmHg, assuming there is no change in temperature?

Solution:

    V1 = 200cm3, P1 = 510mmHg, P2 = 780mmHg V2 = ?

    Using the expression for Boyle’s law:

       P1V1 = P2V2

         V2 = P1V1  = 510mmHg x 200cm3 = 130.769 = 131 cm3

                   P2              780mmHg

2. A certain mass of a gas occupies 300cm3 at 35oC. At what temperature will it have its volume reduced by half assuming its pressure remains constant?

Solution:

V1 = 300cm3, T1 = 35oC = (35 + 273)K = 308K, V2 = V1/2 = 300/2 = 150cm3, T2 = ?

Using the formula for Charles’ law

V1 = V2

       T1    T2

       T2 = V2T1 = 150cm3 x 308K = 154K

                  V1              300cm3

GENERAL GAS EQUATION

Boyle’s and Charles’ laws are combined into a single expression known as the general gas equation which can be expressed mathematically as 

   P1V1 = P2V2

         T1T2

IDEAL GAS EQUATION

This equation states that for an ideal gas, PV/T is a constant.

That is, PV = R (R = molar gas constant)

             T

             PV = RT

That is, for n mole of a gas, the equation becomes

             PV = nRT

 CALCULATIONS

1. What is the volume at s.t.p of a fixed mass of a gas that occupies 700cm3 at 25oC and 0.84 x 105 Nm-2pressure?

    Solution:

   T1 = 273K, P1 = 1.01 x 105Nm-2, T2 = 25oC = (25 + 273) = 298K, P2 = 0.84 x 105Nm-2, 

    V2 = 700cm3, V1 =?

   Using the general gas equation

P1V1 = P2V2

     T1      T2

     V1 = P2V2T1 = 0.84 x 105Nm-2 x 700cm3 x 273K = 533.337 =533cm3

              P1T2          1.01 x 105Nm-2 x 298K

2. Calculate the number of moles present in a certain mass of gas occupying 6.5dm3 at     3atm and 15oC (R = 0.082atmdm3K-1mol-1)

    Solution:

    V = 6.5dm3, P = 3atm, T = 15oC = (15 + 273)K = 288K, n =?

    Using PV = nRT

           n = PV = 3atm x 6.5dm3= 0.8257

                RT    0.082atmdm3K-1mol-1 x 288K

    Number of moles = 0.83 mole

 DALTON’S LAW OF PARTIAL PRESSURE

This law states that in a mixture of gases which do not react chemically together, the total pressure exerted by the mixture of gases is equal to the sum of the partial pressure of the individual gases that make up the mixture.

Mathematically, the law can be expressed as:

     P total = PA + PB +PC……..Pn

Where P total is the total pressure of the mixture and PA, PB, and PC are the partial pressure exerted separately by the individual gases A, B, and C that make up the mixture.

The pressure each constituent gas exerts is called partial pressure and is expressed as

The partial pressure of gas A (PA) = Number of moles of gas A  x total

                  Total number of moles of gas in a mixture

That is, PA = nA x P total

                    nA + nB + nC

If the gas is collected over water, it is likely to be saturated with water vapor and the total pressure becomes

       P total = P gas + P water vapor 

       P gas = P total – P water vapor

CALCULATION ON THE LAW

1. A gaseous mixture containing 64g of O2 and 70g of N2 exerts a total pressure of 1.8oatm. What is the partial pressure exerted by oxygen in the mixture?

Solution:

Molar mass of O2 = 16 x 2 = 32gmol-1

Molar mass of N2 = 14 x 2 = 28gmol-1

Number of mole of O2 = 64g            = 2.0mole

                              32gmol-1

Number of mole of O2 = 70g            = 2.5mole

                                28gmol-1

Total number of moles of gases in mixture = 2.0 + 2.5 = 4.5 mole

Partial pressure of O2 = 2.0 x 1.80 = 0.80atm

                             4.5

 ASSIGNMENT 

1. A given mass of nitrogen is 0.12dm3 at 60oC and 1.01 x 105Nm-2. Find its pressure at the    same temperature if its volume is changed to 0.24dm3
2. 272cm3 of CO2 was collected over water at 15oC and 782mmHg pressure. Calculate the volume of dry gas at s.t.p (saturated vapor pressure of water at 15oC is 12mmHg).

AVOGADRO’S LAW

This law states that an equal volume of all gases at the same temperature and pressure contains the same number of molecules. This means that 1 mole of any gas at s.t.p has a volume of 22.4dm3.

GAY LUSSAC’S LAW OF COMBINING VOLUMES

It states that when gases react they do so in volumes which are simple ratios to one another and the volumes of the products if gaseous, provided that the temperature and pressure remain constant.

CALCULATION ON THE LAW

1. Calculate the volume of oxygen required to burn 500cm3 of methane completely.

 Solution:

 The equation for the reaction is:

      2CH4(g) + 3O2(g) → 2CO2(g) + 2H2O(g)

 By Gay Lussac’s law, 

 2 volumes of CH4 requires 3 volumes of O2 for complete combustion

 Therefore, 2cm3 of CH4 requires 3cm3 of O2

       500cm3 of CH4 will require Xcm3 of O2

   Xcm3 of O2 = 500cm3 x 3cm3 = 750cm3

                2cm3

   Thus, 750cm3 of O2 is required

GRAHAM’S LAW OF DIFFUSION

It states that the rate of diffusion of a gas is inversely proportional to the square root of its density at constant temperature and pressure. 

Mathematically,

            R α 1/√d

            R = k/√d where k is a constant

Comparing the rate of diffusion of two gases:

            R1 = √d2

            R2   √d1

In terms of relative molecular mass, M

            R α 1/√M

For two gases,

            R1 = √M2

            R2   √M1

But the rate of diffusion is reciprocal of time, R =1/t

That is,

            R1 = t2

            R2    t1

From the inverse relationship, we can deduce that the less dense a gas is, the higher the rate of diffusion and vice versa.

CALCULATION

1. A given volume of SO2 diffuses in 60 seconds. How long will it take the same volume of    CH4 to diffuse under the same condition (SO2 = 64, CH4 = 16)

   Solution:

  Using the expression:  

            t1= √M2

            t2   √M1

                        t2 = √M2 x t1 = √16 x 60seconds = 30seconds

                  √M1        √64

ASSIGNMENT

1. State Graham’s law of diffusion
2. Under the same condition of temperature and pressure, hydrogen diffuses 8 times as fast as gas Y. Calculate the relative molecular mass of Y.
3. State the following rule/principle: (a) Hund’s rule of maximum multiplicity (b) Aufbau principle
4. Write the electronic configuration of (a) oxide ion, (b) Aluminium ion,  (c) potassium (d) phosphorus.