Application Of Trigonometric Ratios To Problem Solving SS1 Mathematics Lesson Note

SINE, COSINE AND TANGENT OF ACUTE ANGLES

Given a right-angled triangle, the trigonometric ratio of acute angles can be found as:

1. ABC is any triangle, right-angled at A

tan B  =  b /c 

tan C  = c /b  (tan: Opp)        Adj

Sin B = b  ; Sin C  = c  Sin; Opp

             a                  a

 Cos B  = c  ; Cos C  =  b ( Cos : Adj)

               a                     a

In <ABC, B and C are complementary angles i.e B + C = 90°  

If B =  Ө  then C = 90° – Ө.

sin Ө  = cos ( 90-Ө )  = b/a

Cos Ө  = Sin (90- Ө)  = c/a

Note:  Always remember SOH      CAH   TOA

i.e Sin θ = Opp/Hyp

Cos θ= Adj/Hyp 

Tan O  =Opp/Adj.

Examples

1. A triangle has sides 8cm and 5cm and an angle of 90° between them. Calculate the smallest angle of the triangle 
2. Town Y is 200km from town X in a direction of 40°. How far is Y east of X?

Solutions:

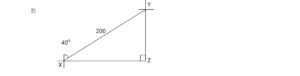
From the diagram drawn above the distance of Y east of X = ZY

Using the right-angled triangle XZY

Sin 40° = ZY

                200km

ZY  = 200km x sin 40°

= 200km x 0.6428

= 128.56km

= 128.6km to 1d.p

CLASSWORK 

1. A ladder 20cm long rests against a vertical wall so that the foot of the ladder is 9m from the wall.

(a) Find, correct to the nearest degree, the angle that the ladder makes with the wall

(b) Find correct to 1. dp the height above the ground at which the upper end of the ladder touches the wall. Use of tables of trigonometric ratios.

DETERMINATION OF LENGTHS OF CHORDS USING TRIGONOMETRIC RATIOS

Trigonometric ratios can be used to find the length of chords of a given circle.  However, in some cases where angles are not given.

Pythagoras theorem is used to find the lengths of chords in such cases.

Pythagoras theorem is stated as follows:

It states that c2 = a2 + b2

Pythagoras’ theorem states that in a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the square of the lengths of the other two sides.

Examples

1. A chord is drawn 3cm away from the centre of a circle of radius 5cm. Calculate the length of the chord.
2. In a figure, O is the centre of the circle, HKL.  HK = 16cm, HL = 10cm and the perpendicular from O to the HK is 4cm.  What is the length of the perpendicular from O to HL?

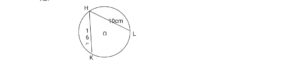
Solution:

1. Sketch a right-angled triangle and label it correctly. 

|AB|^2  + 3^2  = 5^2  ( Pythagoras theorem)

|AB|^2 =  5^2 – 3^2

 |AB|^ 2 = 2^5 – 9

|AB| ^ 2  = 16

 AB    = √16 = 4cm  

Since B is the midpoint of chord AC then: 

Length of chord AC = 2 x AB  

 = 2x 4cm =8cm

2. Let the distance from O to HL= xcm

In right-angled triangle OMH:

 |OH|^2  = |HM|^2   + |MO| ^2

|OH|^2=  8^2 + 4^2

 =  64  + 16 = 80

:.         |OH|  = √80  

:.           OH   = √80cm

 but   OH   = radius of the circle 

i.e r=   OH     =   OL  = √80cm

In a right-angled triangle  ONL

OL  2  =    ON 2   +   NL 2

i.e( √80)2 = x2 + 52

80- 25 = x2

55 = x2

Take the square root of both sides 

√55   = √x2

√55 = x = 7. 416cm 

:. The length of the perpendicular from O to HL is 7.416cm